キバハリアリ(myrmesia)でみる重回帰モデル

明けましておめでとうございます．

早速ですが，今回キバハリアリデータセットを使って重回帰を適用してみます．今回はキバハリアリの頭幅を重回帰モデルで予測を試みます．

今回使用したデータとコードはgithubにあります．

github.com

環境

Windows 10
- conda 4.2.12
  - python 3.5.1
  - pandas 0.18.1
  - scipy 0.18.1
  - statsmodels 0.6.1
  - matplotlib 1.5.1

Problem

「キバハアリの頭幅は各部位の大きさによって決まるのか」という問題を考えます．

キバハリアリの特徴

キバハリアリは，そもそもどういう特徴のアリなのかを引用します．

キバハリアリはオーストラリア大陸およびその周辺に分布（生息）するアリで，キバハリアリ属として知られている，このアリは，"bulldog ants" と呼ばれ，多くのアリ研究者や生物学者の注目を集めている．その理由はキバハリアリがアリ科(family Formicidae)の中でも祖先的な形質を多く持っていて， "原始的"なアリとされているためである．

いくつかの種は"jack jumper" と言われるように，飛び跳ねることができる．

ほとんどの種はかなり攻撃的で，人が刺されるとアレルギーになったり，死ぬことさえある．

NagatomoNakamura, "クラスター化の統計的評価とその応用", 1995年3月, p.130 9.1.キバハリアリの特徴

キバハリアリの外見の特徴は，

(1)非常に大きなあご

(2)発達した複眼と単眼

(3)明瞭に区別される胸部の亜区分

(4)2つの節からなる腹柄

(5)強力で機能的な刺針

NagatomoNakamura, "クラスター化の統計的評価とその応用", 1995年3月, p.130 9.1.キバハリアリの特徴

となっている．

キバハリアリは，以下のような姿をしている．

Fig1. キバハリアリ

ブルドック属 - Wikipedia https://ja.wikipedia.org/wiki/%E3%83%96%E3%83%AB%E3%83%89%E3%83%83%E3%82%B0%E3%82%A2%E3%83%AA%E5%B1%9E

今回，目的変数としているキバハリアリの頭は，以下の形をしている．

Fig2. キバハリアリの頭

ブルドック属 - Wikipedia https://upload.wikimedia.org/wikipedia/commons/2/2c/Bullant_head_detail.jpg"

Plan

データ収集の計画

今回は，既に収集されているデータを使う．重回帰モデルに扱う変数はすべて量的変数とする．

データ解析の計画

$ y $ を頭幅，$ x $ をほかの部位として，重回帰モデル $$ y = \beta_0 + \beta_1 x_{1} + \beta_2 x_{2} + \cdots + \beta_{p}x_{p} + \varepsilon, (p \leq 12), \varepsilon \sim N(0, \sigma^2) $$ で説明できないかを考える．

Data

キバハリアリの各部位を計測したデータセットには，Ogata(1991)氏が測定したものがある．今回は，「NagatomoNakamura, "クラスター化の統計的評価とその応用", 1995年3月, p.197-201, 付録Dキバハリアリの部位測定データ」に載っているデータを使用した．使用したcsvデータはgithubに挙げてあります．

github.com

計測部位（特性，変数）は，$12 $ 個からなる．

全標本数（標本の大きさ）は，$N=252$ になる．

種類

種群(SPGroup)は9つに分かれている． Wikipedeia に書かれている各種の特徴を並べる．

aberrans
cephalotes
gulosa

英名にはGiant bulldog ant、Red bulldog antなどがある。働きアリの体長は15〜26mm。25mmを超えるインチ・アンツの一つ。キバハリアリ亜科全体の基準種であると同時に、オオキバハリアリ亜属の基準種に位置づけられる。
mandibularis
nigrocincta

nigrocincta亜属の基準種。本種もしばしば「ジャック・ジャンパー」と呼ばれることがある。頭部は黒色だが、胸部〜腹部は赤褐色と黒色の大まかな縞模様。大顎、触角、脛節はより明るい赤褐色である。
picta
pilosula

ジャックジャンパーアント亜属の基準種。タスマニア島〜オーストラリア最南端付近に分布する。働きアリの体長は12〜14mm、女王は14〜16mm。体色は若干赤みがかりにぶい光沢のある黒褐色で、脚と触角はやや明るい赤褐色。キバハリアリとしてはやや小型であるが、敵や獲物に飛び跳ねて襲いかかるため、「ジャック・ジャンパー」の渾名で知られる。前方跳躍蟻、ジャンパーに類別されるキバハリアリの最も有名な種の一つ。
tepperi
urens

NagatomoNakamura, "クラスター化の統計的評価とその応用", 1995年3月, p.131 9.2データセットの特徴

計測部位

計測した部位は以下になる．

HW(Head Width):頭幅
HL(Head Length):頭長
SL(Space Length): 柄節長
ML(Mandible Length): 大あご長
WL(Weber's Length of mesosoma): ウェーバーの胸長
PrW(Pronotal width): 前胸幅
HFL(Hind femoral Length): 後脚腿節長
PtW(Petiole Width): 腹柄節幅
PtL(Petiole Length): 腹柄節長
Ppw(Postpetiole Width): 後柄節幅
PpL(Postpetiole Length): 後柄節長
GW(Gastral width):腹部幅

計測値は $20$ で割ると $[mm]$ の単位になる．つまり，$20[mm]$ を1単位として計測している．表の中のデータの "-" は欠損値を表している．

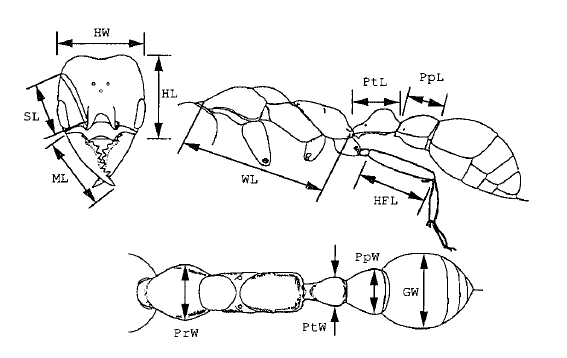
名称だけではわかりずらいので，各部位を図で表したものを引用します．

Analysis

pythonのpandas, scipy, statsmodelsを使って重回帰をする．

頭幅 HW を目的変数
その他の変数を説明変数

とするような重回帰を考える．変数選択をし，もっともよく目的変数を説明できる変数のみを求める．

(1) csvデータの読み込み

まず必要なライブラリを読み込んでおく．


# scipy
import scipy as sp
import scipy.stats as stats

# pandas
import pandas as pd

# statsmodels
import statsmodels.api as sm
import statsmodels.formula.api as smf

# matplotlib
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.font_manager as fm
fp = fm.FontProperties(fname='/Windows/Fonts/YuGothM.ttc')

pandas を使ってcsvデータを読み込む．


myrmesia_df = pd.read_csv("myrmesia_data.csv", encoding="utf-8")
myrmesia_df.head(5)

	ID-SpeciesName	SPGroup	HW	HL	SL	ML	WL	PrW	HFL	PtW	PtL	Ppw	PpL	GW
0	01aberrans	aberrans	59	58	40	47	84	40	60	20	25	34	26	50
1	02aberrans	aberrans	53	53	37	40	77	34	58	18	22	30	24	45
2	03aberrans	aberrans	63	61	41	48	89	40	65	22	25	38	28	55
3	01excavata	aberrans	57	55	37	44	82	39	56	20	25	33	22	48
4	02excavata	aberrans	53	52	35	41	75	35	50	17	22	30	21	43


  # 全標本数を確認
total_n = myrmesia_df["ID-SpeciesName"].count()
total_n

252

欠損値の操作

今回は欠損値のある標本を除外する．

csvデータでは'-' が欠損値なので，Nanに置き換える．


# 欠損値"-"の抽出してNanに置き換え
myrmesia_nan = myrmesia_df.copy()
myrmesia_nan[myrmesia_df=="-"] = sp.nan
myrmesia_nan.head(9)

	ID-SpeciesName	SPGroup	HW	HL	SL	ML	WL	PrW	HFL	PtW	PtL	Ppw	PpL	GW
0	01aberrans	aberrans	59	58	40	47	84	40	60	20	25	34	26	50
1	02aberrans	aberrans	53	53	37	40	77	34	58	18	22	30	24	45
2	03aberrans	aberrans	63	61	41	48	89	40	65	22	25	38	28	55
3	01excavata	aberrans	57	55	37	44	82	39	56	20	25	33	22	48
4	02excavata	aberrans	53	52	35	41	75	35	50	17	22	30	21	43
5	01froggatti	aberrans	66	61	45	51	95	42	66	23	27	40	25	55
6	01maura	aberrans	69	67	43	50	90	44	69	25	27	40	26	59
7	02maura	aberrans	62	62	41	45	88	40	65	21	25	37	22	55
8	03maura	aberrans	65	63	40	50	NaN	NaN	NaN	NaN	NaN	38	NaN	56

DataFrame.dropna()関数で欠損値のある標本を除外する．


#欠損値を除外
myrmesia_remNan = myrmesia_nan.dropna(axis=0)
myrmesia_remNan.head(9)

	ID-SpeciesName	SPGroup	HW	HL	SL	ML	WL	PrW	HFL	PtW	PtL	Ppw	PpL	GW
0	01aberrans	aberrans	59	58	40	47	84	40	60	20	25	34	26	50
1	02aberrans	aberrans	53	53	37	40	77	34	58	18	22	30	24	45
2	03aberrans	aberrans	63	61	41	48	89	40	65	22	25	38	28	55
3	01excavata	aberrans	57	55	37	44	82	39	56	20	25	33	22	48
4	02excavata	aberrans	53	52	35	41	75	35	50	17	22	30	21	43
5	01froggatti	aberrans	66	61	45	51	95	42	66	23	27	40	25	55
6	01maura	aberrans	69	67	43	50	90	44	69	25	27	40	26	59
7	02maura	aberrans	62	62	41	45	88	40	65	21	25	37	22	55
9	01forrnosa	aberrans	62	60	41	47	87	40	65	20	24	34	25	48

量的データをint型へ変換する．


# 数値データをintへ変換
myrmesia_remNan_int = myrmesia_remNan.copy()
myrmesia_remNan_int[["HW", "HL", "SL", "ML", "WL", "PrW", "HFL", "PtW", "PtL", "Ppw", "PpL", "GW"]] = myrmesia_remNan.iloc[:, 2:].astype(int)

myrmesia_remNan_int.dtypes

ID-SpeciesName    object
SPGroup           object
HW                 int32
HL                 int32
SL                 int32
ML                 int32
WL                 int32
PrW                int32
HFL                int32
PtW                int32
PtL                int32
Ppw                int32
PpL                int32
GW                 int32
dtype: object


# 標本数を確認
n = myrmesia_remNan_int["ID-SpeciesName"].count()
n

99

欠損値のない標本99個であったことがわかる．

基本（記述）統計量を計算

DataFrame.describe() 関数で基本統計量をみる．


myrmesia_remNan_int.describe()

	HW	HL	SL	ML	WL	PrW	HFL	PtW	PtL	Ppw	PpL	GW
count	99.000000	99.000000	99.000000	99.000000	99.000000	99.000000	99.000000	99.000000	99.000000	99.000000	99.000000	99.000000
mean	48.949495	46.555556	39.979798	46.040404	78.656566	34.252525	57.888889	19.777778	24.171717	31.656566	22.484848	45.838384
std	9.190028	8.190615	7.492826	7.498189	12.686295	6.548630	11.203943	3.869176	3.953919	6.465231	4.250723	8.360142
min	23.000000	23.000000	19.000000	23.000000	41.000000	15.000000	29.000000	10.000000	14.000000	15.000000	10.000000	22.000000
25%	44.000000	43.000000	36.500000	43.000000	72.000000	30.000000	53.500000	18.000000	22.000000	28.000000	20.000000	41.500000
50%	49.000000	47.000000	40.000000	47.000000	82.000000	35.000000	59.000000	20.000000	25.000000	31.000000	23.000000	45.000000
75%	55.000000	50.000000	45.000000	50.000000	88.000000	39.000000	65.000000	22.500000	27.000000	35.500000	25.000000	50.000000
max	69.000000	67.000000	55.000000	63.000000	97.000000	48.000000	82.000000	29.000000	34.000000	47.000000	33.000000	67.000000

量的データなので，各散布をみてみる．pandasの場合，scatter_matrix()関数で散布図行列を描いてくれる．


%matplotlib inline

pd.tools.plotting.scatter_matrix(myrmesia_remNan_int, figsize=(7,7), grid=True)
plt.suptitle("Fig. ScatterMatrixPlot of myrmesia measurement", y=0, fontsize=14)
plt.show()

どの変数も正の相関があることがわかる．$12 \times 12 $の相関係数行列を求めます．


myrmesia_remNan_int.corr()

	HW	HL	SL	ML	WL	PrW	HFL	PtW	PtL	Ppw	PpL	GW
HW	1.000000	0.959212	0.727289	0.779383	0.878143	0.956496	0.752532	0.823289	0.769129	0.882624	0.833379	0.926137
HL	0.959212	1.000000	0.711152	0.713412	0.866725	0.888452	0.767482	0.732271	0.747560	0.793887	0.786740	0.870408
SL	0.727289	0.711152	1.000000	0.873805	0.901756	0.728793	0.910752	0.625300	0.836738	0.601027	0.671827	0.755955
ML	0.779383	0.713412	0.873805	1.000000	0.848662	0.809835	0.764182	0.775155	0.857812	0.724168	0.802318	0.765176
WL	0.878143	0.866725	0.901756	0.848662	1.000000	0.886995	0.907666	0.743277	0.887321	0.788177	0.804483	0.883363
PrW	0.956496	0.888452	0.728793	0.809835	0.886995	1.000000	0.742914	0.891044	0.795159	0.943223	0.888162	0.949264
HFL	0.752532	0.767482	0.910752	0.764182	0.907666	0.742914	1.000000	0.596369	0.796040	0.623804	0.664276	0.784178
PtW	0.823289	0.732271	0.625300	0.775155	0.743277	0.891044	0.596369	1.000000	0.759568	0.927784	0.855986	0.876483
PtL	0.769129	0.747560	0.836738	0.857812	0.887321	0.795159	0.796040	0.759568	1.000000	0.714057	0.824946	0.776912
Ppw	0.882624	0.793887	0.601027	0.724168	0.788177	0.943223	0.623804	0.927784	0.714057	1.000000	0.868284	0.928559
PpL	0.833379	0.786740	0.671827	0.802318	0.804483	0.888162	0.664276	0.855986	0.824946	0.868284	1.000000	0.838961
GW	0.926137	0.870408	0.755955	0.765176	0.883363	0.949264	0.784178	0.876483	0.776912	0.928559	0.838961	1.000000

ststsmodelsで回帰モデル

実際にstatsmodelsで回帰モデルを作る． R-likeにモデルを指定するには，statsmodels.formula.api.ols()関数が使える．

http://statsmodels.sourceforge.net/devel/example_formulas.html

formula='HW ~ HL + SL + ML + WL + PrW + HFL + PtW + PtL + Ppw + PpL + GW のようにすれば，目的変数をHWとして，説明変数を $HL, SL, ML, WL, PrW, HFL, PtW, PtL, Ppw, PpL, GW$ と定数項で表すモデルを作る．


lmodel = smf.ols('HW ~ HL + SL + ML + WL + PrW + HFL + PtW + PtL + Ppw + PpL + GW', data=myrmesia_remNan_int.loc[:, "HW":"GW"])

modelの中のfit()関数でモデル（回帰式）の結果が返ってくる．


fit = lmodel.fit()
fit.summary()

OLS Regression Results
Dep. Variable:	HW	R-squared:	0.977
Model:	OLS	Adj. R-squared:	0.974
Method:	Least Squares	F-statistic:	330.2
Date:	Sat, 31 Dec 2016	Prob (F-statistic):	6.04e-66
Time:	19:06:03	Log-Likelihood:	-173.67
No. Observations:	99	AIC:	371.3
Df Residuals:	87	BIC:	402.5
Df Model:	11
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[95.0% Conf. Int.]
Intercept	-2.1434	1.130	-1.897	0.061	-4.389 0.102
HL	0.6395	0.048	13.389	0.000	0.545 0.734
SL	0.0286	0.083	0.345	0.731	-0.136 0.193
ML	0.1405	0.063	2.247	0.027	0.016 0.265
WL	-0.0924	0.059	-1.556	0.123	-0.210 0.026
PrW	0.6575	0.119	5.544	0.000	0.422 0.893
HFL	-0.0437	0.041	-1.066	0.289	-0.125 0.038
PtW	-0.1563	0.134	-1.170	0.245	-0.422 0.109
PtL	0.0281	0.110	0.256	0.798	-0.190 0.246
Ppw	0.0996	0.115	0.868	0.388	-0.128 0.328
PpL	-0.2194	0.095	-2.305	0.024	-0.409 -0.030
GW	0.1130	0.082	1.379	0.171	-0.050 0.276

変数をすべて ( 12 ) 含んだ回帰式の性能は，

寄与率 $0.977$
自由度調整済寄与率 $0.97365$
AIC(12) = $371.3$


# 自由度調整済寄与率
fit.rsquared_adj
0.97365260334015702


# AIC
fit.aic
371.34322280217464

変数選択

F値を使う手法もあるが，今回はAICを使って，変数選択を行う． stastmodels では，AIC(定数項あり)は， $$ AIC(df_{model}) = -2 \ln{lf} + 2(df_{model} + 1). $$ おそらく，多項式の回帰は， $$ AIC(p) = n \ln (2\pi \frac{S_e}{n}) + n + 2df_{model} $$ - $S_e$: 残差平方和 - $df_{model}$: 自由パラメータ数で計算している．

statsmodels.regression.linear_model.RegressionResults — statsmodels 0.7.0 documentation

残差平方和は，fit()関数の返り値 statsmodels.regression.linear_model.RegressionResults.ssr で求められる．

AICを求める関数を定義してみる．


def AIC_polynomial(n, p, Se):
  return n * sp.log(2 * sp.pi * Se / n) + n + 2 * p

> AIC_polynomial(99, 12, fit.ssr)
371.34322280217464

AICはモデルの粗雑さを表すので，小さい値がいいモデルを表す． Rには総当たりでAICが最も小さいモデルを返すstep関数がある． statsmodelsにはないので自分で書く．


# 参考：http://stackoverflow.com/questions/22428625/does-statsmodels-or-another-python-package-offer-an-equivalent-to-rs-step-f

import itertools

def step(df, model):
  '''
  Returns:
      - Dataframe:
          index = pair exog
          columns = AIC, F0, adj.R^2
  '''
  exog = sp.array(model.exog_names)
  exog = exog[exog!="Intercept"]
  candi_exogs = []
  AICs = []
  for k in range(1,len(exog)+1):
      for candi_exog in itertools.combinations(exog, k):
          # Combination of exogs
          predictors_df = df[list(candi_exog)].copy()
          predictors_df['Intercept'] = 1
          res = sm.OLS(model.endog, predictors_df).fit()
          candi_exogs.append(str(candi_exog))
          AICs.append([res.aic, res.fvalue, res.rsquared_adj])
  return pd.DataFrame(AICs, columns=["AIC", "F0", "R2_adj"], index=candi_exogs)

AICの昇順を求めると


aic_df = step(myrmesia_remNan_int, lmodel)
aic_df.sort_values("AIC").head()

	AIC	F0	R2_adj
('HL', 'ML', 'WL', 'PrW', 'PpL', 'GW')	364.432664	620.074977	0.974295
('HL', 'ML', 'WL', 'PrW', 'HFL', 'PpL', 'GW')	365.106519	532.980602	0.974358
('HL', 'ML', 'WL', 'PrW', 'PpL')	365.163714	731.205548	0.973860
('HL', 'ML', 'WL', 'PrW', 'Ppw', 'PpL')	365.334548	614.312728	0.974060
('HL', 'ML', 'PrW', 'HFL', 'PpL', 'GW')	365.387105	613.978555	0.974046

AICが最も小さかった時の変数は，以下の6つであった．

HL(Head Length):頭長
ML(Mandible Length): 大あご長
WL(Weber's Length of mesosoma): ウェーバーの胸長
PrW(Pronotal width): 前胸幅
PpL(Postpetiole Length): 後柄節長
GW(Gastral width):腹部幅


opt_model = smf.ols(formula="HW ~ HL + ML + WL + PrW + PpL + GW", data=myrmesia_remNan_int)
opt_fit = opt_model.fit()
opt_fit.summary()

OLS Regression Results
Dep. Variable:	HW	R-squared:	0.976
Model:	OLS	Adj. R-squared:	0.974
Method:	Least Squares	F-statistic:	620.1
Date:	Sat, 31 Dec 2016	Prob (F-statistic):	4.27e-72
Time:	19:06:10	Log-Likelihood:	-175.22
No. Observations:	99	AIC:	364.4
Df Residuals:	92	BIC:	382.6
Df Model:	6
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[95.0% Conf. Int.]
Intercept	-1.9965	1.020	-1.957	0.053	-4.023 0.030
HL	0.6304	0.044	14.299	0.000	0.543 0.718
ML	0.1235	0.042	2.910	0.005	0.039 0.208
WL	-0.1006	0.034	-2.980	0.004	-0.168 -0.034
PrW	0.7042	0.094	7.525	0.000	0.518 0.890
PpL	-0.2100	0.080	-2.611	0.011	-0.370 -0.050
GW	0.0965	0.060	1.604	0.112	-0.023 0.216

得られた回帰モデルは，以下のようになる．幅と長さの項をまとめると，$WL, PpL$ は偏回帰係数はマイナスなので，ほかの変数との差になっている可能性があります．

$$ \hat{HW} = -2 + 0.6 HL + 0.1 ML -0.1 WL + 0.7 PrW - 0.2 PpL + 0.1 GW \ = 0.1 { (7 PrW + GW) + ( (6HL + ML) - (WL + 2 PpL ) ) -20 } $$

残差とテコ比の検討

回帰モデルの妥当性を検討するために，残差のt値ととテコ比をみて外れ値がないかをみる．

残差と標準化残差と残差のt値を以下のように計算できる． $$ e_i = y_i - \hat{y_i} $$ $$ e'_{i} = \frac{e_i}{\sqrt{\hat{sigma^2}}} \sim N(0, 1^2) $$ $$ et_i = \frac{e_i}{\sqrt{1 - h_{ii}} \hat{\sigma^2}} \sim t(df=n-p-1) $$

残差のt値はt分布に従うので，t分布から外れている値を外れ値として判定できる．テコ比の目安は，$h_{kk} < 2.5 \times \bar{h_{kk}} $になっているかで判断する方法がある[2]．

残差のt値とテコ比は，可視化するだけであれば， statsmodelsのstatsmodels.graphics.influence_plot()関数で描画できる．横軸がテコ比，縦軸が残差のt値になる．influence plot では，残差のt値とテコ比が共に大きい場合，scatterが大きく描画される．


%matplotlib inline
fig, ax = plt.subplots(figsize=(12,8))
fig = sm.graphics.influence_plot(opt_fit, ax=ax)

plt.hlines([-3, 3], 0, 0.5, colors="red")
plt.hlines([-2.5, 2.5], 0, 0.5, colors="yellow")

leverage_warning = 2.5 * (6+1) / n
plt.vlines(leverage_warning, -3.5, 3.5, colors="red")

plt.grid()
plt.xlim(0, 0.25)
plt.ylim(-3.5, 3.5)
plt.show()

残差のt値の観点からみると，t分布の全体の$95\%$から外れている標本は， $$ num(e_t > t(\alpha=0.05/2, df=\phi_e)=1.986) = 7 $$ No. 5, 14, 16, 245, 193, 233, 12 である．99個中7個より今回は大きくずれているとは判断しない．

テコ比の観点からみると，テコ比の目安は， $$ h_{kk} > 2.5 \times \bar{h_{kk}} = 0.17676 $$ となる．外れている標本は3つだが，特別大きく外れていると判断しない．

回帰式の利用

取得したデータが，作った回帰モデルの予測区間から外れていないかをチェックする．

信頼率$100\alpha [\%] $予測区間は， statsmodels.sandbox.regression.predstd import wls_prediction_std(res=fit, alpha=alpha) 関数で計算できる．

誤差棒付きでプロットする．信頼率$95\%$ の予測区間をみると，大きく外れている標本はないことを確認できる．

次に，新しい標本を取得して， HW以外を測定できたとき， $$ HL = 58, ML = 47, WL=84,PrW=40,Ppl=26, GW=50 $$ のとき，$HW$ はどのような値で予測できるかをみる．なお，これらの値はSample No.0を参考にした．

信頼率95%信頼区間は， $$ \hat{HW} = -2 + 0.6 HL + 0.1 ML -0.1 WL + 0.7 PrW-0.2 PpL + 0.1 GW $$ より，信頼区間 $$ \hat{HW} \pm t(\phi_e, \frac{\alpha}{2}) \sqrt{(\frac{1}{n} + \frac{D²}{n-1}) \hat{\sigma²}} $$ (D²)は，マハラノビス距離の二乗より， $$ D² = (\vec{x} - \vec{\mu})^T \boldsymbol{\Sigma}^{-1} (\vec{x} - \vec{\mu}) \ \vec{x} = \begin{pmatrix} HL \ ML\ WL \ PrW \ PpL \ GW \end{pmatrix} $$

平均ベクトルは $ pandas.mean() $ 関数で求める． $\ boldsymbol{\Sigma}^{-1}$ は各変数の分散共分散行列の逆行列になる．分散共分散行列は$pandas.cov()$関数で計算できる．


# myrmesia_remNan_int[["HL", "ML", "WL", "PrW", "PpL", "GW"]]
Sigma = sp.asmatrix(myrmesia_remNan_int[["HL", "ML", "WL", "PrW", "PpL", "GW"]].cov().as_matrix())
Sigma

matrix([[  67.0861678 ,   43.81405896,   90.0600907 ,   47.65419501,
           27.39115646,   59.60090703],
        [  43.81405896,   56.22284065,   80.72830344,   39.76520305,
           25.572047  ,   47.96578025],
        [  90.0600907 ,   80.72830344,  160.9420738 ,   73.68965162,
           43.38249845,   93.68882705],
        [  47.65419501,   39.76520305,   73.68965162,   42.88455988,
           24.72325294,   51.96980004],
        [  27.39115646,   25.572047  ,   43.38249845,   24.72325294,
           18.06864564,   29.81385281],
        [  59.60090703,   47.96578025,   93.68882705,   51.96980004,
           29.81385281,   69.89198103]])

マハラノビス距離の二乗を求める関数を関数を作る．


def Mahala2(vec_x, vec_mean, mat):
    length = mat.shape[0]
    vec = sp.asmatrix((vec_x - vec_mean).reshape(length, 1))
    inv = sp.linalg.inv(mat)
    mahala2 = vec.T.dot(inv.dot(vec))
    return mahala2[0, 0]

同様にして，予測区間は， $$ \hat{HW} \pm t(\phi_e, \frac{\alpha}{2}) \sqrt{(1 + \frac{1}{n} + \frac{D^2}{n-1}) \hat{\sigma^2}} $$ で求められる．

信頼区間と予測区間をプロットする．今回は，$HL$以外の変数を固定として，$HL$を横軸にして，目的変数$HW$ をみる．


  # HLを変えた予測値
%matplotlib inline
plt.figure(figsize=(4.5, 4.5))

# plt.scatter(x1, y)

hl_l = sp.linspace(20, 70, 100)
hat_y = []
# hl以外変数固定
(ml, wl, prw, ppl, gw) = (47, 84, 40, 26, 50)
for hl in hl_l:
    X = sp.array([1, hl, ml, wl, prw, ppl, gw])
    hat_y.append(X.dot(opt_fit.params))
plt.plot(hl_l, hat_y)

# interval
phi_e = n - opt_fit.df_model - 1
t_0025 = stats.t.isf(q=0.05/2, df=phi_e)
# マハラノビス距離の二乗
vec_mean = myrmesia_remNan_int[["HL", "ML", "WL", "PrW", "PpL", "GW"]].mean() # 平均ベクトル
D2 = []
for hl in hl_l:
    D2_0 = Mahala2([hl, ml, wl, prw, ppl, gw], vec_mean, Sigma)
    D2.append(D2_0)
D2 = sp.array(D2)

interval095 = t_0025 * sp.sqrt((1/n + D2 / (n-1)) * opt_fit.scale)
plt.plot(hl_l, hat_y - interval095, "--g", label="95% interval conf.")
plt.plot(hl_l, hat_y + interval095, "--g")

pred_interval095 = t_0025 * sp.sqrt((1 + 1/n + D2 / (n-1)) * opt_fit.scale)
plt.plot(hl_l, hat_y - pred_interval095, "--r", label="95% prediction conf.")
plt.plot(hl_l, hat_y + pred_interval095, "--r")

# sample HL=58 のとき
hl=58
X = sp.array([1, hl, ml, wl, prw, ppl, gw])
plt.scatter(hl, X.dot(opt_fit.params), color="k", )

plt.grid()
plt.axis("scaled")
plt.xlim(20, 70)
plt.ylim(20, 70)
plt.xlabel("HL")
plt.ylabel("HW")
plt.title("plot Confidence in fixing ML, WL, PrW, PpL, GW", y=- 0.2)
plt.legend(loc=4)
plt.tight_layout()
plt.show()

結論

キバハリアリは体が大きいと顔幅$HW$も大きくなりそうです．

AICが最も小さくなるモデルから,$HW$を決めるのに関係ありそうな変数は，$PrW, GW, HL, ML, WL, PpL $ の6つでした．

重回帰モデルでの回帰式は， $$ \hat{HW} = 0.1\{(7 PrW + GW) + ( ( 6HL + ML) - (WL+2PpL) ) -20\} $$

自由度調整済み寄与率は，$0.974$より，このモデルで $HW$ を $ 97.4 [%] $ 説明できていることになる．

今回は種類をまとめて分析しましたが，種類別で分析するともっと性能の高い会期モデルを作れるかもしれません（標本は減りますが）

はしくれエンジニアもどきのメモ

情報系技術・哲学・デザインなどの勉強メモ・備忘録です。

キバハリアリ(myrmesia)でみる重回帰モデル

キバハリアリ(myrmesia)でみる重回帰モデル

環境

Problem

キバハリアリの特徴

Plan

データ収集の計画

データ解析の計画

Data

種類

計測部位

Analysis

(1) csvデータの読み込み

欠損値の操作

基本（記述）統計量を計算

ststsmodelsで回帰モデル

変数選択

残差とテコ比の検討

回帰式の利用

結論