ハノイの塔問題メモ
import scipy as sp
import matplotlib.pylab as plt
規則¶
- 1回に1枚の円盤だけ動かす.
- 移動の途中で円盤の大小を逆に積んではいけない. 常に大きい方の円盤が下になるようにする.
- 棒A,B,C以外のところに円盤を置いてはいけない.
ハノイの塔($n=3$段)の目標
1 1
22 -> 22
333 333
場所A 場所B 場所C 場所A 場所B 場所C初期状態
1
22
場所A 場所B 場所C1回目:1段目 A->B
22 1
場所A 場所B 場所C2回目:2段目 A->C
1 22
場所A 場所B 場所C3回目:1段目 B->C
1
22
場所A 場所B 場所C初期状態
1
22
333
場所A 場所B 場所Cまず,[1-2]段を場所Bに逃がす
1回目:1段目 A->C
22
333 1
場所A 場所B 場所C2回目:2段目 A->B
333 22 1
場所A 場所B 場所C3回目:1段目 C -> B
1
333 22
場所A 場所B 場所C避難完了したので,3段目を場所Cへ
4回目:1段目 A -> C
1
22 333
場所A 場所B 場所C2段目を場所$C$へ移動させるため, [1]段を避難させる
5回目:1段目 B -> A
1 22 333
場所A 場所B 場所C避難できたので,2段目を場所Cへ
6回目:2段目 B -> C
22
1 333
場所A 場所B 場所C7回目:1段目 A -> C
1
22
333
場所A 場所B 場所C初期状態
1
22
333
4444
場所A 場所B 場所Cまず,[1-3]段を場所Bに逃がす. そのため,3段目を場所Bに置くことを考える.
1回目:1段目 A->B
22
333
4444 1
場所A 場所B 場所C2回目:2段目 A->C
333
4444 1 22
場所A 場所B 場所C3回目:1段目 B -> C
333 1
4444 22
場所A 場所B 場所C3段目を場所Bへ
4回目:3段目 A -> B
1
4444 333 22
場所A 場所B 場所C避難させていた[1-2]段を場所$C$から場所Bへ
5回目:1段目 C -> A
1
4444 333 22
場所A 場所B 場所C6回目:2段目 C -> B
1 22
4444 333
場所A 場所B 場所C7回目:1段目 A -> B
1
22
4444 333
場所A 場所B 場所C避難完了したので,4段目を場所Cへ
8回目:4段目 A -> C
1
22
333 4444
場所A 場所B 場所C場所Bの3段目を場所Cへ移動させることを考える. そのため,[1-2]段を場所Aへ避難させる.
9回目:1段目 B -> C
22 1
333 4444
場所A 場所B 場所C10回目:2段目 B -> A
1
22 333 4444
場所A 場所B 場所C11回目:1段目 C -> A
1
22 333 4444
場所A 場所B 場所C[1-2]段の避難ができたので, 3段目を場所Cへ
12回目:1段目 B -> C
1 333
22 4444
場所A 場所B 場所C2段目を場所Cへ動かすことを考える.
13回目:1段目 A -> B
333
22 1 4444
場所A 場所B 場所C[1]段の避難ができたので,2団目を場所Cへ移動
14回目:2段目 A -> C
22
333
1 4444
場所A 場所B 場所C移動完了
15回目:1段目 B -> C
1
22
333
4444
場所A 場所B 場所C考え方¶
n段ハノイの塔を徳手順を考える.
Hanoi(k, s, p, g): k段の円盤を場所 $s$ から 場所 $g$ へ 途中,場所pを介しながら円盤を移動する手順とする.
コード¶
def hanoi(n:int, start:str, partition:str, goal:str):
'''
n段をstart->goalへ移動.
partitionは途中の移動に使用
'''
if n >= 1:
# 上に乗っているn-1段を一旦移動
hanoi(n-1, start, goal, partition)
print("{} 段目を {} -> {} ".format(n, start, goal))
# 一旦移動したn-1段をgoalへ
hanoi(n-1, partition, start, goal)
hanoi(3, "A", "B", "C")
関数呼び出しを追う¶
n=2の場合¶
Hanoi(2, f, w, d)
{
Hanoi(1, f, d, w)
{
print(1: f -> w)
}
print(2: f -> d)
Hanoi(1, w, f, d)
{
print(1: w -> d)
}
}n=3の場合¶
Hanoi(3, f, w, d)
{
Hanoi(2, f, d, w)
{
Hanoi(1, f, w, d)
{
print(1: f -> d)
}
print(2: f -> w)
Hanoi(1, d, f, w)
{
print(1: d -> w)
}
}
print(3: f -> d)
Hanoi(2, w, f, d)
{
Hanoi(1, w, d, f)
{
print(1: w -> f)
}
print(2: w -> d)
Hanoi(1, f, w, d)
{
print(1: f -> d)
}
}
}01 def hanoi(n:int, start:str, partition:str, goal:str):
02 if n >= 1:
03 hanoi(n-1, start, goal, partition) # 上に乗っているn-1段を一旦移動
04 print("{} 段目を {} -> {} ".format(n, start, goal))
05 hanoi(n-1, partition, start, goal)ここでHanoi(n,start, partition, goal) という操作の意味を正確にしておく。
- この操作は $1-n$ まで順に積まれた $n$ 個の円盤を
startからgoalへ移動する操作。 - 操作開始時,
startには $1 - n$ まで順に積まれた $n$ 個の円盤がある。 - 操作終了後,
goalには$1 - n$まで順に円盤が積まれたものになる。 - その際,
partitionを補助的に使っても良い。 - さらに,この操作はゲームの規則(1),(2),(3) を満たす。
- またn+1 以上の円盤があっても,この操作はそれに関係なく行われる。
証明は数学的帰納法を使う。
-
$n=0$ の場合: 2行の条件を満たさないから,
Hanoi(n, s, p, g)は何もしない。 -
$n=1$ の場合: $n=1$ の場合,$3-5$行が実行されるが, 3,5行は
Hanoi(0,s, g, p),Hanoi(0, p, s, g)で何も実行しません。つまり,この場合は,4行だけ実行されます。従って,1番の円盤をstartからgoalへ移動と言う操作で,この場合正しい操作になっています。 -
$n-1$の場合: Hanoi が正しい操作を行っていると仮定します。 このとき $n$の場合正しい操作になることを示す。
- まず,開始時
startには $1 - n$ まで順に積まれた$n$個の円盤がある。 2. 03行目で,Hanoi(n-1, s, g, p):このとき,startには $1 - n$ までの円盤があるから,この操作は可能。 ここで Hanoi はn-1の時は正しい操作をすると言う仮定から,3行の結果,$1 - n-1$ までの円盤が規則(1),(2),(3) を満たしながらpへ移動する。 この過程で $1 - n-1$ 以外の円盤の上に乗ることもありますが,あったとしても, それは $n$ 以上の大きいものの上です。 従って規則(2)を満たす。 - 次に,04行目で $n$番目の円盤を
sからgへ移動する。今 $1 - n-1$までの円盤はpにあるから,goalに円盤があるとしてもそれは$n + 1$番以上の円盤です。従って,$n$の円盤をgに移動しても規則(2)を満たす。
- まず,開始時
-
最後に,5行目で
Hanoi(n-1, p, start, goal): これは先ほど移動した,$1 - n-1$ の円盤をpからgoalに移動するもの。 これもHanoi は $n-1$ の時は正しい操作をすると言う仮定から,正しく動作し,規則(2)を満たす。
以上から,nの場合も正しい操作になる。
移動回数¶
def hanoi(n:int, start:str, partition:str, goal:str):
move_n = 0
def hanoi_rec(n:int, start:str, partition:str, goal:str):
'''
n段をA->Bへ移動.
Cは途中の移動に使用
'''
if n >= 1:
# nonlocal でローカル変数でないことを宣言
# https://docs.python.jp/3/faq/programming.html
nonlocal move_n
# 上に乗っているn-1段を一旦移動
hanoi_rec(n-1, start, goal, partition)
print("{} 段目を {} -> {}".format(n, start, goal))
# 一旦移動したn-1段をgoalへ
hanoi_rec(n-1, partition, start, goal)
move_n = move_n + 1
hanoi_rec(n, start, partition, goal)
print("move_n: ", move_n)
hanoi(3, "A", "B", "C")
hanoi(5, "A", "B", "C")
移動回数の計算¶
参考: http://www2.cc.niigata-u.ac.jp/~takeuchi/tbasic/BackGround/Hanoi.html
ハノイの塔の解法プログラム Hanoi での移動の回数を計算。 移動の回数を $H(n)$ と表す。
Hanoi(n, s, p, g)は 3,4,5行で移動を出力するが,
- 3行は $H(n-1)$ 回の移動,
- 4行は 1回の移動,つまり,$H(1)$
- 5行は $H(n-1)$回の移動を出力します。
従って, $H(1)=1, n >1$ のとき,
$$ H(n)=H(n-1)+1+H(n-1) $$となる。
この漸化式は, $H(1)=1, n>1, H(0)=0$ のとき,
$$ H(n) = 2 \cdot H(n-1) + 1 \\ H(n) + 1 = 2 \cdot H(n-1) + 2 \\ H(n)+1 = 2 \cdot (H(n-1)+1) $$$$ \{H(1)+1 = 2, 2(H(1)+1), 2^2 (H(1)+1), \cdots \} $$から初項$H(1)+1 = 2$, 公比$r=2$ の等比数列より,
$$ H(n)+1 = (H(1)+1) \cdot 2^{n-1} \\ = 2^n\\ $$よって,
$$ H(n)=2^n - 1 $$となる.
メルセンヌ素数 https://ja.wikipedia.org/wiki/%E3%83%A1%E3%83%AB%E3%82%BB%E3%83%B3%E3%83%8C%E6%95%B0 と一致する.
def H(n):
n_int64 = sp.array(n, dtype=sp.int64)
return sp.power(2, n_int64) - 1
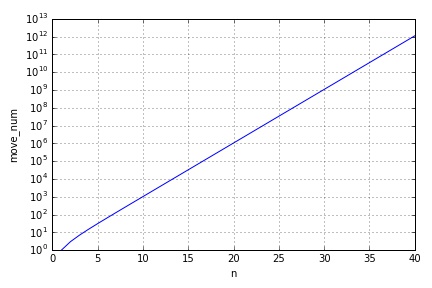
この数値はかなり大きい。
例えば,
- $H(10)=1023$
- $H(40)=1099511627775$
となる。
H(10), H(40)
%matplotlib inline
n_ar = sp.arange(1, 40+1, 1)
plt.plot(n_ar, H(n_ar))
plt.yscale("log")
plt.xlabel("n")
plt.ylabel("move_num")
plt.grid()
plt.show()
H(n_ar)
Hanoi(3, f, w, d)
{
Hanoi(2, f, d, w)
{
Hanoi(1, f, w, d)
{
print(1: f -> d)
}
print(2: f -> w)
Hanoi(1, d, f, w)
{
print(1: d -> w)
}
}
print(3: f -> d)
Hanoi(2, w, f, d)
{
Hanoi(1, w, d, f)
{
print(1: w -> f)
}
print(2: w -> d)
Hanoi(1, f, w, d)
{
print(1: f -> d)
}
}
}を参考にスタックとwhileループを利用して実装する.
def hanoi_ite(n, f, w, d):
stack = []
# now
(N, From, Work, Dist) = (n, f, w, d)
stack.append((N, From, Work, Dist))
while stack:
while N-1 >= 1:
# N-1段を F -> W
stack.append((N-1, From, Dist, Work))
(N, From, Work, Dist) = stack[-1]
# N段を F -> D
p = stack.pop()
print(p)
(N, From, Work, Dist) = p
if N-1 >= 1:
# N-1段を W -> D
stack.append((N-1, Work, From, Dist))
(N, From, Work, Dist) = stack[-1]
hanoi_ite(5, "A", "B", "C")
def hanoi_ite(n, f, w, d):
stack = []
# now
(N, From, Work, Dist) = (n, f, w, d)
stack.append((N, From, Work, Dist))
while stack:
while N-1 >= 1:
# N-1段を F -> W
stack.append((N-1, From, Dist, Work))
(N, From, Work, Dist) = stack[-1]
# N段を F -> D
p = stack.pop()
# print(p)
(N, From, Work, Dist) = p
if N-1 >= 1:
# N-1段を W -> D
stack.append((N-1, Work, From, Dist))
(N, From, Work, Dist) = stack[-1]
def hanoi(n:int, start:str, partition:str, goal:str):
'''
n段をstart->goalへ移動.
partitionは途中の移動に使用
'''
if n >= 1:
# 上に乗っているn-1段を一旦移動
hanoi(n-1, start, goal, partition)
# print("{} 段目を {} -> {} ".format(n, start, goal))
# 一旦移動したn-1段をgoalへ
hanoi(n-1, partition, start, goal)
import time
n = 20
time_rec = []
time_ite = []
def get_time(func, args_tuple, loop=5):
times = []
for i in sp.arange(loop):
s = time.time()
func(*args_tuple)
e = time.time()
times.append(e - s)
return sp.mean(times)
for i in sp.arange(1, n+1, 1):
time_rec.append(get_time(hanoi, (i, "A", "B", "C")))
time_ite.append(get_time(hanoi_ite, (i, "A", "B", "C")))
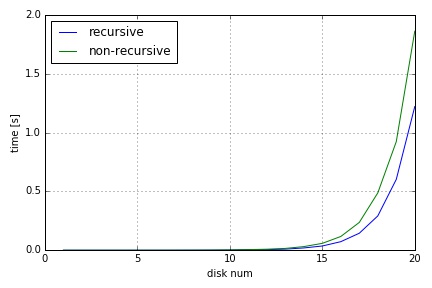
plt.plot(sp.arange(1, n+1, 1), time_rec, label="recursive")
plt.plot(sp.arange(1, n+1, 1), time_ite, label="non-recursive")
plt.xlabel("disk num")
plt.ylabel("time [s]")
plt.suptitle("measuring time: recursive vs non-recursive", y=0)
plt.legend(loc=2)
plt.grid()
plt.tight_layout()
plt.show()
参考¶
- 大槻共著, "エンジニアのためのプログラミング入門" 2007年, p.160 ハノイの塔

エンジニアのためのプログラミング入門―VB.NETによるプログラミングの基礎
- 作者: 大槻正伸,内田修司,山田貴浩,小泉康一,島村浩
- 出版社/メーカー: 電気書院
- 発売日: 2007/03
- メディア: 単行本
- この商品を含むブログを見る