R言語で多変量解析４（正規分布、確率密度関数、正規分布の標準化）

正規分布の描画

１変数の標準正規分布の確率密度関数を[ -5, +5 ]の範囲で描画。

 curve( dnorm( x, mean=0, sd=1 ), xlim = c( -5, 5 ), lwd = 5 )

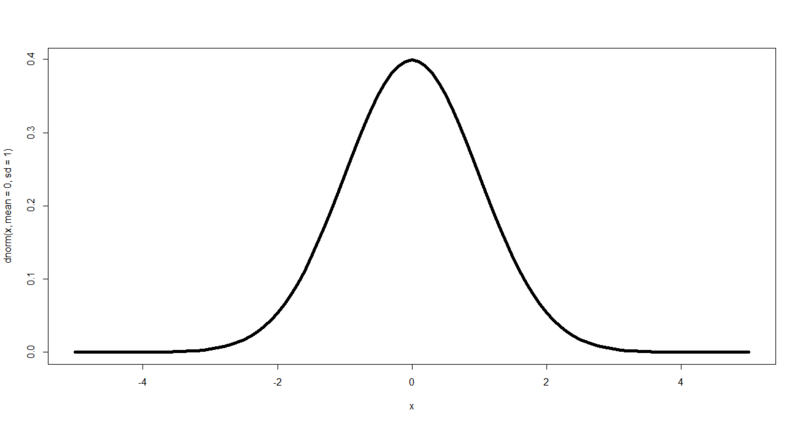
確率密度関数

確率密度関数：サンプル数を無限にした時に得られる曲線と横軸のなす面積が１となるように正規化した関数。

• サンプルデータがたくさん集まった場合、ヒストグラムで観察することが多い。

例：

 rnorm(n)：正規分布に従う乱数を n 個生成

> x <- rnorm( n=100 )
> hist( x )

 x <- rnorm( n=10000 )
hist( x )

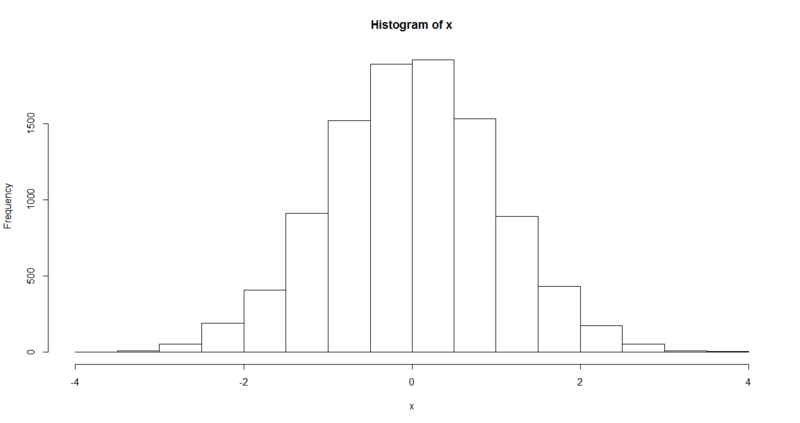
正規分布するデータをランダムに発生させて散布

x <- rnorm( n=3000 )
y <- rnorm( n=3000 )
plot(x, y)

 標準偏差を変えてみる

curve( dnorm( x, sd=0.7 ), xlim = c( -4, 4 ), lwd = 4, col = "black" )
curve( dnorm( x, sd=1 ), xlim = c( -4, 4 ), lwd = 4, col = "red", add = TRUE )
curve( dnorm( x, sd=2 ), xlim = c( -4, 4 ), lwd = 4, col = "blue", add = TRUE )

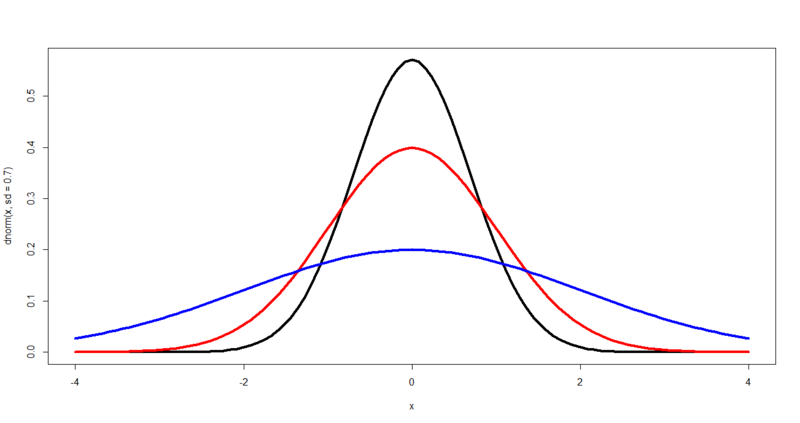
正規分布の標準化

• N( μ, σ^2 )からN( 0, 1 )への変換

　　　　

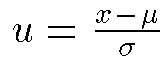
• Pr(u≧k) = Pのように、標準正規分布でkからPを求めたり、Pからkを求めるための統計数値表があるが、Rでも同様なことができる

• pnorm( k )：kより左側の面積(確率)を返す

k <- 2.0
P <- 1 - pnorm( k )
pnorm( k )
[1] 0.9772499
P
[1] 0.02275013

• qnorm( P )：面積Pとなる左側のk値。lower.tail=FALSEで右側のk値。

P <- 0.5
k <- qnorm( P )
k
[1] 0
P <- 0.1
k <- qnorm( P )
k
[1] -1.281552
k <- qnorm( P, lower.tail=FALSE )
k
[1] 1.281552